User manual - Filament Wound Tube Stress Analysis from Cadfil
 Cadfil Help contents
Cadfil Help contents  Cadfil.com Home
Cadfil.com Home
Overview
From Cadfil the 'Tube Stress Analysis' menu option should be selected from The 'Utilities' menu. The user interface is very simple and consists of a single window dialog box as show below. There are four groups of dialog controls, Material properties, Loads, Geometry and the Action buttons which are described below.

Material properties
The left column has the 11 material properties, first there are four material stiffness parameters (engineering constants), these are properties for the Unidirectional (a single fibre direction) composite.
Ex is the modulus in the direction of the fibre. This properties is largely governed by the fibre properties.
Ey is the transverse modulus, that is the stiffness in the direction at 90 degrees to the fibre direction. This property is
largely governed
by the resin as that is what holds the fibres together.
vx the Poisson's Ratio in the fibre direction
G is the shear Modulus
The modulus properties are measured in Pascal Pa (N/m2), the Poisson's ratio is dimensionless.
Fibre Volume fraction is the percentage (by volume) of the composite that is fibre. This is not currently used in any analyses but
it is useful to keep this value in mind as if your actual volume fraction is significantly different then the other material properties
are likely to be not representative data for your material.
Density Ro is the density of the composite measured on kg/m3, this is used to calculate the mass off the pipe and is also important
for the natural frequency calculation (for example if the tube is a drive shaft and might whirl).
The then follow 5 strength parameters for the Unidirectional composite
Tx - Is the tensile strength in the fibre direction
Cx - Is the compressive strength in the fibre direction
Ty - Is the tensile strength in the transverse direction
Cy - Is the compressive strength in the transverse direction
SS - Is the shear strength
The strength parameters are all specified in Pa (N/m2). A good introduction to the strength and analysis of composite materials and a more detailed explanation of the unidirectional material parameters can be found in [1]. It cannot be stressed strongly enough that any analysis is worthless if the material data is not representative. Different fibres, resin, volume fraction and processing conditions can give rise to entirely different properties. Also, you need to be mindful of the environmental conditions of the item you are designing as some material properties can be significantly influenced by factors such as temperature and humidity. There is no substitute for actually measuring the properties of the materials you are using under your own processing conditions. There is a good review of test methods and test standards for measuring the required properties of filament wound materials to be found in chapter 8 of [2].
You will note that there is a 'pull down' box at the top of the left hand column that allows material data to be selected from a database. If you want to use your own material data you will need to add it to the material database. This a is simple file in CSV (comma separated value) format that is best modified in Microsoft Excel or some other spread sheet program. The database is found in the Cadfil installation folder (usually called C:\Cadfil\cadfil7xx) and has the name cadfil_material_data.csv. The database has three types of data Fibre data, resin data and composite data. Fibre and resin data can be used in the creation of winding programs, the tube stress program is only interested in the "composite" data and ignores all other data in the file. The format for a composite unidirectional material record is "Composite", "UD_mate", description, Ex, Ey, vx, G, Vol frac, Density, Tx, Cx, Cy, SS. The first item in this case the word 'Composite' is in column A, the text 'UD_Mate' in column B, a description or name for the material (up to 80 characters long) in column C. The next 11 columns have the material values as described above. If you edit or modify the file remember to save it as csv format not excel format.
Load Cases
There are 7 load cases and the user can have any combination of these. The loads as named in respect of an axis system where 'x' is along
the axis of the pipe (axial), 'y' is perpendicular to 'x' and 'z' is perpendicular to both 'x' and 'y'.
Axial Tension - the Is specified in Newton (N) and is in the X direction i.e. along the axis of the tube
and is assumed to be spread evenly over the cross section. For compressive axial forces use a negative number.
Y-Shear and Z-Shear are transverse shear forces in the Y and Z directions (normal to the tube axis)
and it is assumed that the load is spread evenly over the cross section. If both shear
forces are specified these are combined
(resolved) in a single shear force using good old Pythagoras.
Torque - Specified in Nm this a twisting moment about the axis of the tube and important load for drive shafts for example.
Y-Bending and Z-Bending are bending moments about the Y and Z directions applied to the tube ends considering the tube as a beam,
these are Specified in Nm. If both moments are specified these are combined
(resolved) in a single moment using good old Pythagoras.
Internal Pressure - Specified in Pa (N/m2). The resulting stresses assume that the cylinder has closed ends,
that is the pressure gives rise to both and axial and a hoop
stresses using classical thin shell theory. If an external pressure is required use a negative
pressure which will give rise to compressive stresses.
Geometry
There are 4 parameters in this group, Inside Diameter (m), Wall thickness (m), Length (m) and Wind Angle
(degrees). The length is used for calculating
the tube mass and for the buckling and natural frequency calculation, if you are not interested in these values the default value of 1m can be used. The inside
diameter of the tube is
the outside diameter of the mandrel used for the winding.
The wind angle is for angle angle ply that is a +/- angle layup with 0 degrees being axial and 90 being hoop.
Button controls
Buttons are used for actions and are:
Help - This opens the specific help pages for this option
Save - This saves the material selection, loads and geometry to a text file, the text file is then opened in the default text editor (normally Windows Notepad).
The text file is given a default name (stress_input.txt) so if you want to keep it do a 'Save As' to give it a meaningful name.
You must close the text file before you can proceed with the software. This option is useful if you want a permanent
record of your input data.
Open - This allow the user to pick a text file previously created with 'Save'. The date is loaded as input in the dialog and can then be used or modified.
Cancel - This exits from the option and back to the Cadfil main menu, the 'X' box in the top right corner of the dialog has the same effect.
Calculate Modulus v Angle - This option calculates material properties as a function of wind angle and is
discussed in the next section.
Calculate Pipe Stress - This option calculate stresses, strains, and factors of safety for the different load cases and is
discussed in a later section.
Modulus / wind angle output
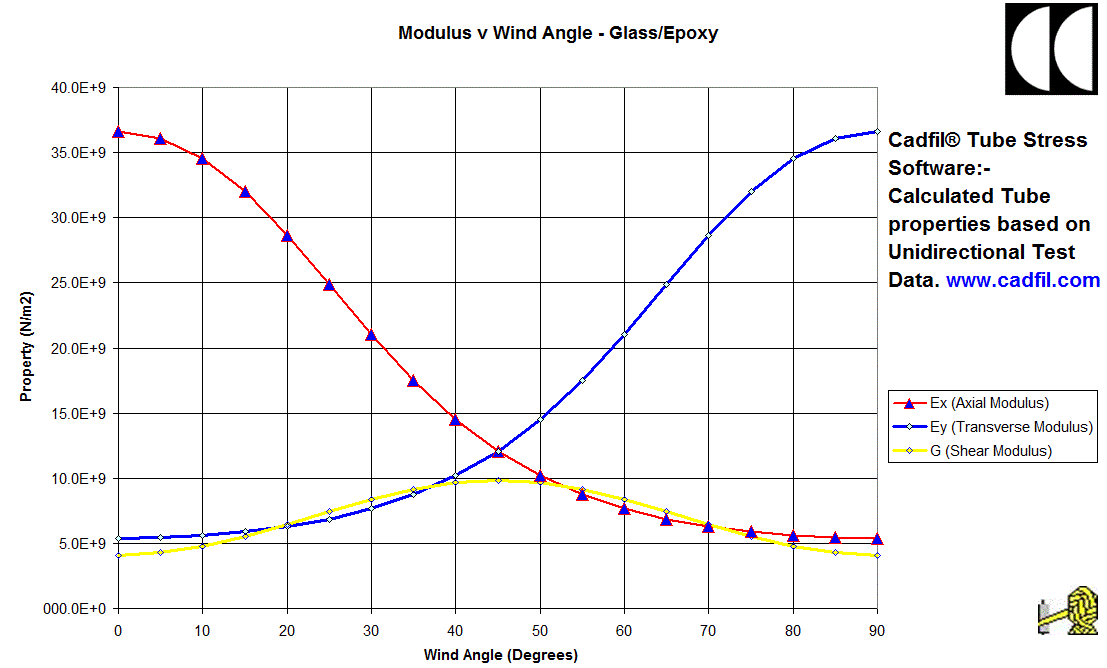
When the Calculate Modulus v Angle button is pressed the software uses thecuurent material data an calaculates in pane stiffness compliance matrices (both standard and normalised) and equivalent engineering constants for angle-ply laminates over the full 0 degree to 90 degree range in steps of 5 degrees. This data is ouput in tabulated form to a text file called 'modulus_angle_data.txt' which is then opened in the default text editor. This data can be saved with an appropraite name or can be pasted into an Excel spreadsheet. The software comes with a standard template Excel 2003 file so if the data is pasted into this a series of ready made and fully formated graphs are avialable. Some Sample output of such a is shown graphed is shown to the left. This shows how the tube axial, hoop and shear moduli vary with wind angle. The data is based for an E-Glass /Epoxy unidirectional engineering properties from physical test data of filament wound tubes. This data was taken form the standard database of data supplied with the software. A number of published sets of data are included in the data base for glass and some more exotic filament types. The user can easily add their own material test data to the database.
Stress, Strain and factor of safety (FOS) and other output
Some typical stress output is shown in the table (text file) shown below, a detail reference explaining all the terms and for those that need to know the theoretical basis of he calculation with references can be found in the help files.
----------------------------------------------------------------------------------------------------
Cadfil Pipe Stress Module V1.0
Results for the analysis of a composite tube
Units are Strict SI - Distance [m], Stress/Stiffness [N/m2], Area [m2], Section Inertia [m4]
----------------------------------------------------------------------------------------------------
GEOMETRY
Length of Tube : 8.000E+00
Outside diameter : 306.000E-03
Inner diameter : 300.000E-03
Thickness : 3.000E-03
Angle of Plies(+/-): 55.000E+00
MATERIAL DATA
Material Name : E-Glass/Epoxy-48%-(PPG 72GPa) ISSN1819-6608 Vol3 No4 Aug 2008
Density : 1.528E+03
Ex 0 degree Modulus: 36.600E+09
Ey 90 deg. Modulus: 5.400E+09
vx Poissons Ratio : 300.000E-03
G shear Modulus : 4.090E+09
CALCULATED PROPERTIES
Mass : 34.908E+00
Area : 2.856E-03
IXX (J) : 65.551E-06
IYY=IZZ (I) : 32.776E-06
ZY : 214.220E-06
KY : 211.428E-03
E1 (axial) : 8.739E+09
E2 (hoop) : 17.477E+09
v12 (axial v) : 309.844E-03
v21 (trans v) : 619.671E-03
Shear Modulus : 9.150E+09
Eeq : 12.358E+09
veq : 438.179E-03
Fn (nat. freq. Hz) :
60Fn (1/min) :
LOADS
Axial load : 4.000E+03
Torque : 500.000E+00
Resolved Shear : 0.000E+00
Resolved Bending : 0.000E+00
Internal Pressure : 0.000E+00
ASSUMPTIONS.
The Package Uses Thin Shell Theory For Pressure Loads.
Y-Y And Z-Z Bending Moments Are Resolved By Pythagoras.
Maximum And Minimum Bending Stresses Are Considered Independently.
No Local Bending Is Considered In The Laminate.
Constant Strain Through The Laminate Thickness.
Quadratic Failure Criteria To Calculate Strength Ratios.
Normalised Interaction Term Assumed As -1/2.
Cowper s Formula Used To Calculate Shear Coefficient.
UTS Taken As Strength Of Unidirectional Composite.
Cross-Over Effects In Layers Are Ignored.
IN-PLANE STRESSES SIG1 SIG2 SIG6
Negative Bending Moment 1.4007E+06 0.0000E+00 1.1670E+06
Positive Bending Moment 1.4007E+06 0.0000E+00 1.1670E+06
PRINCIPLE IN-PLANE STRESSES SIGP1 SIGP2
Negative Bending Moment 2.0614E+06 -660.6911E+03
Positive Bending Moment 2.0614E+06 -660.6911E+03
IN-PLANE STRESS INVARIANTS I R PHASE
Negative Bending Moment 700.3517E+03 1.3610E+06 29.5156E+00
Positive Bending Moment 700.3517E+03 1.3610E+06 29.5156E+00
INTER-LAMINA SHEAR SIGXZ
Negative Bending Moment 0.0000E+00
Positive Bending Moment 0.0000E+00
IN-PLANE STRAINS e1 e2 e6
Negative Bending Moment 160.2877E-06 -49.6641E-06 127.5426E-06
Positive Bending Moment 160.2877E-06 -49.6641E-06 127.5426E-06
ON-AXIS MATERIAL STRAINS ex ey es
Negative Bending Moment Negative Angle Layer -40.5175E-06 151.1411E-06 153.6681E-06
Negative Bending Moment Positive Angle Layer 79.3333E-06 31.2903E-06 -240.9124E-06
Positive Bending Moment Negative Angle Layer -40.5175E-06 151.1411E-06 153.6681E-06
Positive Bending Moment Positive Angle Layer 79.3333E-06 31.2903E-06 -240.9124E-06
ON-AXIS MATERIAL STRESSES SIGX SIGY SIGS
Negative Bending Moment Negative Angle Layer -1.2548E+06 760.6236E+03 628.5024E+03
Negative Bending Moment Positive Angle Layer 2.9940E+06 301.4908E+03 -985.3315E+03
Positive Bending Moment Negative Angle Layer -1.2548E+06 760.6236E+03 628.5024E+03
Positive Bending Moment Positive Angle Layer 2.9940E+06 301.4908E+03 -985.3315E+03
FOS FOR ON-AXIS STRESSES +SIGX -SIGX +SIGY -SIGY SIGS
500.994E+00 1.195E+03 52.588E+00 0.000E+00 69.012E+00
STRENGTH RATIOS FOR GIVEN ON-AXIS STRAINS R R`
Negative Bending Moment Negative Angle Layer 44.218E+00 -149.438E+00
Negative Bending Moment Positive Angle Layer 54.870E+00 -83.940E+00
Positive Bending Moment Negative Angle Layer 44.218E+00 -149.438E+00
Positive Bending Moment Positive Angle Layer 54.870E+00 -83.940E+00
CRITICAL BUCKLING STRESSES TORCR1 TORCR2 SIGCR
(TORSION METHODS 1 AND 2 AND COMPRESSION)
Negative Bending Moment 8.741E+06 9.783E+06 155.639E+06
FOS ON CRITICAL BUCKLING TORCR1 TORCR2 SIGCR
(TORSION METHODS 1 AND 2 AND COMPRESSION)
Negative Bending Moment 7.490E+00 8.383E+00 0.000E+00
Positive Bending Moment 7.490E+00 8.383E+00 0.000E+00
FOS ON INTER-LAMINA SHEAR BASED ON UTS OF
DIRECTIONAL LAYER
Negative Bending Moment 0.000E+00
Positive Bending Moment 0.000E+00
----------------------------------------------------------------------------------------------------
Calculated Properties
The Calculated properties are listed and described below:
Mass - Is just a result of the volume of material( cross section x length x density) and is in Kg.
Area - Area of the tube cross section in m2. Area= Π.(OD^2-ID^2)/4 , ID is inner diameter, OD is outer diameter , OD=ID+2t when t is the wall thickness.
IXX - The Moment of Inertia of the section (J)(m4) about the axis of the tube (x axis), IXX=Π.(OD^4-ID^4)/32
IYY - The Moment of Inertia of the section (I)(m4) about the axis normal the tube axis (y or z axis), IYY=IZZ=Π.(OD^4-ID^4)/64
ZY - Section constant [m3] "I/r" = IXX/OD
KY - Shear constant for thin walled cylinder from Cowper's Formula [3]
E1 (axial) - Modulus of the pipe in the axial direction [N/m2]
E2 (hoop) - Modulus of the pipe in the hoop direction [N/m2]
v12 (axial v) - Poisson's ration the pipe in the axial direction
v21 (trans v) - Poisson's ration the pipe in the hoop direction
Shear Modulus - The shear Modulus [n/m2] of the pipe
Eeq - Equivalent or 'average' modulus for this pipe using √(E1.E2), this is used
for the 2nd and 3rd buckling calculations which are intended or isotropic materials and as such as included as 'ball park' guide values.
veq - Equivalent or 'average' Poisson's ratio for the pipe using √(v12.v21), see the comments above.
Fn (nat. freq. Hz) This is the first natural frequency of the pipe
considering it as a pin ended beam using standard formula found in many basic text books using
the axial modulus of the pipe (E1), IYY, length and mass per unit length. This is a typical case for drive shafts with self aligning bearings.
60Fn ( 1/min) This is the same as Fn above but multiplied by 60 give a more user friendly 'rpm' value for a rotating shaft rather than a frequency in Hz.
Stress and factors of Safety (FOS) Output Descriptions
Please note that where positive bending or negatice bending is reffered to this is due to bending the tube as a beam leading to compressive stresses on one side and tensile stresses on the other. As in some case the tensile and comprssive properties of the composite may not be the same both cases are evaluated and the worst case must be considered by the designer.
IN-PLANE STRESSES: SIG1,SIG2,SIG6 These are the material stresses in the plane of the laminate shell/membrane with respect to the axis of the tube , that is axial, hoop and in-plane shear
PRINCIPLE IN-PLANE STRESSES: SIGP1,SIGP2 These are the principle minimum and maximum material stress which in general will not be aligned with the axis idf the tube.
IN-PLANE STRESS INVARIANTS: I,R,PHASE Are the Mohr's Circle Representation of the in-plane stresses with the 2 invariants and the phase angle (to the tube axis) in degrees. A detailed discussion of the concepts in the 3 sections above can be found in [1].
INTER-LAMINA SHEAR: SIGXZ: This is the interlamina shear stress, but should be treated with some caution for 2 reasons, firstly the wound structure is built up of interwoven strands not laminated plies and secondly this value relies on the shear constant value of which there are numerous different calculations and a considrable anmmount of accademic work and debate. The methode used is by no means 'state of the art'.
IN-PLANE STRAINS: e1,e2,e6: These are the material strains in the plane of the laminate shell/membrane with respect to the axis of the tube , that is axial, hoop and in-plane shear
ON-AXIS MATERIAL STRAINS: ex,ey,es: These are the strains in the fibres in the 0, 90 and shear senses.
ON-AXIS MATERIAL STRESSES: SIGX,SIGY,SIGS: These are the stresses in the fibres in the 0, 90 and shear senses.
FOS FOR ON-AXIS STRESSES: +SIGX,-SIGX,+SIGY,-SIGY,SIGS: These compare the on axis material stresses (both tensile + and compressive -) to the unidirectional strength data that the user selected. The larger the value the safer the design, values less than 1.0 imply failure though any system with an FOS of 1.0 could never be considered safe, normal design engineering principals should be applied!.
STRENGTH RATIOS FOR GIVEN ON-AXIS STRAINS: R,R`: These are the factors of safety (considered the lowest value) for the quadratic formulation of Tsai in strain space [1]. This is a classical laminate theory failure criteria.
CRITICAL BUCKLING STRESSES (TORSION METHODS 1 AND 2 AND COMPRESSION): TORCR1,TORCR2,SIGCR: These are the critical buckling stresses using three different calculations, method one is torsional buckling by our own method, the theoretical basis of which is described elsewhere, method 2 is torsional buckling using a method in Roark using equivalent moduli. This final value is a compressive buckling also using equivalent moduli. Refer to Table 35, case 15a and 17a P689 of [4] for these last 2 cases.
FOS ON CRITICAL BUCKLING TORSION METHODS 1 AND 2 AND COMPRESSION): TORCR1,TORCR2,SIGCR: These are factors of safety for the three buckling cases above.
FOS ON INTER-LAMINA SHEAR BASED ON UTS OF DIRECTIONAL LAYER: Exactly what is says, UTS= ultimate tensile strength!
An example discussion for a drive shaft can be found here.
References
[1] Introduction to composite materials, Stephen W. Tsai, H. Thomas Hahn, Westport Conn. USA, Technomic Publishing, 1980.
[2] Composite Filament Winding, Stan Peters, ASM International, 2011, ISBN 1615037225, 978-1615037223
[3] The shear coefficient in Timoshenko’s beam theory, G. R. Cowper, J. Appl. Mech. ASME, 48, 335-340 (1966)
[4] Roark's Formulas for Stress and Strain, Warren C. Young, Mcgraw-Hill (Tx), 6th edition (January 1, 1989),ISBN 0070725411, 978-0070725416
[an error occurred while processing this directive]